
Ashwood, Melbourne, Australia (2010–11); Washington, DC, United States (2021–22)
(posted April 23, 2010; revised January 18, 2011; updated June 12, 2021)
Abstract
I propose that volume data should be stored, retrieved, processed, and visualized in a “top-down” manner, using pyramid encoding (mipmapping), exploiting the state-of-the-art Magic Kernel Sharp resizing algorithm. The same method can also be used to upsample and downsample in the temporal direction for time-varying datasets.
Most volume data is handled in a “bottom-up” manner, namely, the voxel data at the full captured or computed resolution is considered to be the primary data, and multi-resolution pyramids—where they are used at all—are generally derived from this primary data in an extra processing step, for the purposes of more rapid visualization through progressive refinement.
In this paper I argue that top-down pyramid encoding (mipmapping) is practicable for volume data, using the industry-leading Magic Kernel Sharp resizing algorithm.
Since 2006 I have successfully applied this “top-down” philosophy to two-dimensional images (dubbed JPEG-Clear). In this paper I show its generalization to three-dimensional volume data.
In the following example I have made use of the Drishti volume rendering application, and a sample scan of a stag beetle, 494 x 832 x 832 voxels of byte-valued data (342 MB uncompressed, or 13.3 MB when compressed with gzip; the data is included at the bottom of this page):

Original volume
Downsampling this volume data once (by a factor of two in each direction) using Magic Kernel Sharp yields the following 247 x 416 x 416 representation (42.7 MB uncompressed, 1.82 MB compressed):

Downsampled once
Downsampling again yields the following 124 x 208 x 208 (note that dimensions are rounded up when they are halved) representation (5.36 MB uncompressed, 256 KB compressed):

Downsampled twice
Despite only having 1/64 of the data of the original representation (or 1/52 in compressed form), this representation is still useful. Downsampling again yields the following 62 x 104 x 104 representation (671 KB uncompressed, 40.4 KB compressed):

Downsampled three times
At only 1/512 of the data of the original representation (1/329 compressed), this approximation is arguably still useful. Downsampling again yields the following 31 x 52 x 52 representation (83.8 KB uncompressed, 6.75 KB compressed):
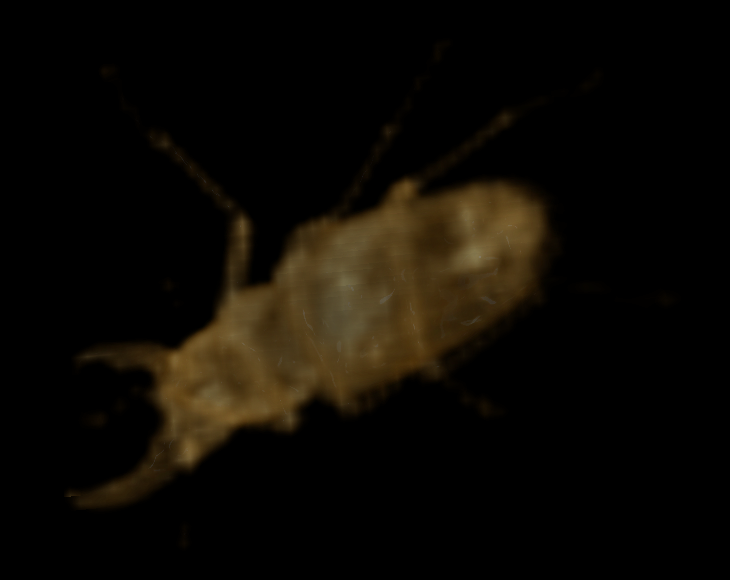
Downsampled four times
This is arguably useful as a low-resolution representation. A further downsampling, to the following 16 x 26 x 26 representation (10.8 KB uncompressed, 1.32 KB compressed), pushes the usefulness of the downsampled representation to its practical limit:

Downsampled five times
Pushing it one more level, to the following 8 x 13 x 13 representation (1.37 KB uncompressed, 330 bytes compressed), yields an object too amorphous for the renderer to generate any useful visual representation (arguably a reasonable limitation, for only 330 bytes of actual information):

Downsampled six times
The example above suggests that it may be useful for a visualization tool to generate the lower-resolution magic kernel representations of an object after loading in the full-resolution dataset. However, pyramid encoding (mipmapping) allows us to turn this multi-resolution pyramid upside-down (or right side up, one could argue): a visualization tool can not only get these approximations essentially for free, but moreover can access them without needing to access the full-resolution dataset at all.
Although not useful for visualization purposes, consider a continuation of the downsampling process for the example shown in the previous section: we successively get a 4 x 7 x 7 representation (196 bytes), a 2 x 4 x 4 representation (32 bytes), a 1 x 2 x 2 representation (4 bytes), and finally a 1 x 1 x 1 representation (1 byte).
I shall refer to this ultimate, single-voxel representation—inside which the entire beetle is contained—as the fundamental voxel, and also as the scale-0 representation. It is essentially the spatial average value of the original dataset.
Let us now (conceptually, at least) store this scale-0 representation in its own data file. The data we store will in general only be an approximation, due to round-off in each downsampling (which depends on the number of bits per voxel we use for each successive representation, which need not be the same at each scale; in the above example, I have stored each representation in byte-valued arrays); and we might also, in general, choose to lossily encode the data before storing it, to save space. I shall refer to what is stored as the scale-0 approximation.
We now use Magic Kernel Sharp to upsample the scale-0 approximation to 1 x 2 x 2 voxels, which I shall refer to as the upsampled scale-0 approximation. We now compute the difference between the scale-1 representation and the upsampled scale-0 approximation, which I shall refer to as the scale-1 diff. We now store the scale-1 diff in its own file.
Again, this diff might, in general, be lossily encoded. We therefore reload and decode the scale-1 diff, and add the result to the upsampled scale-0 approximation, to yield the scale-1 approximation. This is the best approximation that can be reconstructed, at scale 1, using only the two data files that we have stored.
We now iterate this process until we get up to the resolution of the original representation (which, for this example, is scale 10). At each scale, we store only the diff file. (The scale-0 approximation can be also be considered a “diff” from an initial approximation of zero.)
I propose that this set of diff files be used as a complete replacement for the original full-resolution dataset. (If the original dataset must be able to be retrieved losslessly, but lossy encoding has been used for the diffs, then the storage of an additional, losslessly-encoded “final diff,” between the final-scale representation and the final-scale approximation, will suffice.)
In practice, of course, the minimum scale stored would not be scale 0, but rather something more closely aligned with the minimum file size that can be efficiently stored on the file system used (say, scale 5).
From an information theory perspective, it is clear that the Shannon information contained in the set of diffs is equal to that contained in the original dataset; thus, if we are clever enough in our encoding, the amount of storage required for the diff file set should be roughly the same as would be required for the original dataset.
For example, considered in Fourier space, the lower half of the Fourier spectrum (in each direction) of the scale-n representation should be simply the Fourier spectrum of the scale-(n − 1) representation (as it has simply been resampled onto a new lattice with half the lattice spacing), so that the lower half of the Fourier spectrum of the scale-n diff should be zero. (In practice, edge effects, and the difference between the particular generation of Magic Kernel Sharp used and the Fourier-ideal sinc function, means that the lower half of the spectrum will be only approximately zero, but this viewpoint is still illustrative.)
This general property also strongly suggests that encodings exploiting Fourier space—whether lossy or lossless—are likely to be the simplest to implement (at the possible expense of decoding speed). But even a naive implementation in position-space can get sufficiently close to the theoretical limit for practical purposes: such a (lossless) implementation for the stag beetle example above yields a gzipped diff file set of 15.8 MB, compared to the 13.3 MB of the original dataset.
It is also evident that the vast majority of the data size comes from the final diff. Now, since the lower diffs are already providing such an excellent approximation (thanks to the remarkable properties of Magic Kernel Sharp), a practical implementation may choose to encode the final diff far more lossily, if storage space is at a premium, to get the best trade-off between representational fidelity and storage requirements.
Now, clearly, a visualization tool only needs to read in the diff files up to the scale it wishes to render, making progressive refinement lightning-fast: a “thumbnail” can be loaded and rendered essentially instantaneously, regardless of how large the final-scale dataset for that particular object happens to be. Indeed, diff files for different scales can be stored in different directories, or even on physically different storage devices or networks. Extra scales can be loaded in, behind the scenes, when the rendering load is light, and dropped again when the rendering load becomes heavy.
The top-down approach also lends itself to a more efficient storage paradigm for extremely large datasets. Imagine that our original dataset is 100,000 x 100,000 x 100,000 voxels. For most visualization purposes, it will be rare to require all of the quadrillion voxels at the same time: a 1024 x 1024 x 1024 subvolume (or 2048, or 4096, say: pick your favorite number) is likely to be sufficient to exhaust most display resolution requirements. Thus, when visualizing the entire object, it should be rare to need more than scales 0 through 10 (or 11 or 12). Higher scales would only be needed when zooming in on a subvolume.
With this in mind, it makes sense to partition each higher-scale dataset into 1024 x 1024 x 1024 subcubes, and store the scale-n diff for each subcube in its own file. The visualization tool will then never need to load up the files for more than eight such subcubes. The top-down paradigm makes such a “gigavoxel file” model possible at every scale—regardless of whether the entire dataset contains a quadrillion voxels, or indeed any higher power of ten.
In the Appendix I define the concept of top-down coordinates, which provides conceptual and technical assistance in writing the compute code for view volumes at any scale using the top-down storage paradigm.
A side-benefit of using Magic Kernel Sharp is that the set of diffs usefully segments the information in the original volume data into the information at each scale. Visualizing each separate diff may therefore be of use in applications such as medical imaging.
As a naive example, if we simply render the volume obtained from storing the absolute value of each diff value, then at scale 6 we find the following:

Visualization of the diff at scale 6
At scale 7 we find the following:
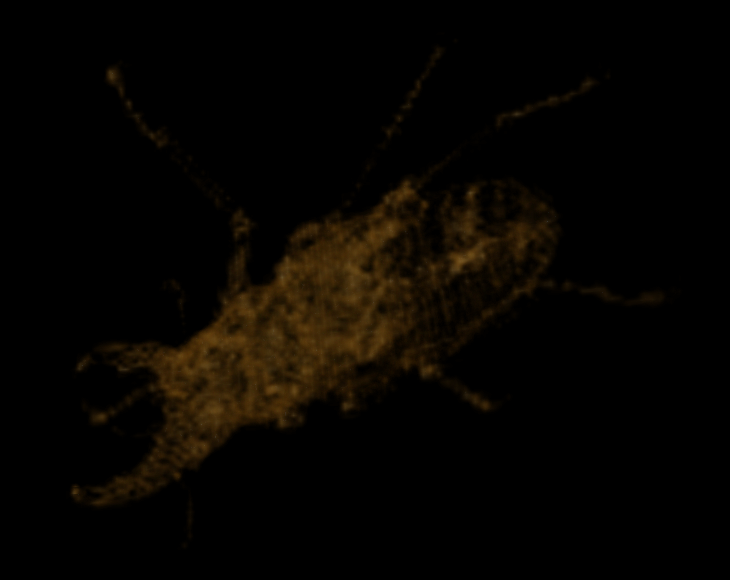
Visualization of the diff at scale 7
At scale 8 we find the following:

Visualization of the diff at scale 8
And at scale 9 we find the following:

Visualization of the diff at scale 9
(For this example, there is little information at the original scale 10, suggesting that the original data was effectively upsampled from scale 9.) This is an extremely efficient way of visualizing the interior of objects at different scales, which we get for free when we use Magic Kernel Sharp in this way.
To this point, we have only considered the use of Magic Kernel Sharp in the representation of the volume data. However, the same philosophy may be fruitfully employed in all aspects of the visualization pipeline.
For example, if only a low-resolution representation of an object has been loaded from storage, then an equivalently low-resolution rendering engine can be launched, to yield a similarly low-resolution rendered two-dimensional image. This low-resolution image can then up upsampled using Magic Kernel Sharp, yielding an optimally upsampled image to match the display resolution.
Because three-dimensional rendering engines are not, in general, linear operations, upsampling the rendered image will not, in general, be equivalent to rendering the upsampled volume data: these two operations will not, in general, commute. However, they may be sufficiently commutative for practical use, or the alternatives may be useful for different purposes.
In the (3+1)-dimensional case of time-varying volume data, Magic Kernel Sharp can be fruitfully used to upsample and downsample in the temporal direction. However, the typical uses of temporal upsampling and downsampling are fundamentally different to those of the spatial directions, and so it is important to not try to treat such datasets as simply having four spatial dimensions, but to rather keep the time direction completely isolated from the spatial directions. Simply put: store the volume data at each time step as per the above description; do not (in general) downsample in the time direction before storing the data.
Temporal upsampling can be used to provide a “slow motion” view that does not “jump” from frame to frame. Slowing down time by any factor can be obtained by simply piping the data through the appropriate upsampling filter. This upsampling may be done on either the volume data or on the rendered images; again, the two methods will not yield identical results if the rendering engine is sufficiently nonlinear.
Likewise, temporal downsampling can be used to provide rapid “cue and review“ capabilities, without needing to skip any frames in the process.
In this paper I have proposed a paradigm for the storage and processing of image data that should allow implementers of visualization systems to provide maximal responsiveness and rendering power for end-users, for any given set of hardware constraints. I have implemented the proposal in ANSI C (see below), and have shown that it delivers on its promises through an illustrative example.
I gratefully acknowledge the kind assistance of Ajay Limaye in the use of the wonderfully simple Drishti volume rendering application, and for providing me with the sample volume dataset used in this paper.
The reference implementation of the above is contained in the following ANSI C code:
There are two sample programs included:
There are also 73 executables of unit tests and death tests provided.
Instructions for building the code are contained in the _README file within the archive.
Note that all code provided here is from my personal codebase, and is supplied under the MIT License.
The sample beetle data used in the examples above is contained in the following file:
If you like this 3D generalization of JPEG-Clear, then you may also find useful the following image processing resources that I have put into the public domain over the decades:
Using the conventional bottom-up paradigm for volume data, the three integers that identify a given voxel are just the array coordinates, namely, k ∈ [0, depth), j ∈ [0, width), and i ∈ [0, height). These ranges are mapped to physical coordinates using a dimensionful scale factor for each direction.
In the top-down paradigm, however, there is a separate voxmap for each scale. At first sight, this suggests a tedious transformation of voxel coordinates as we move from scale to scale. For example, for the beetle above, the dimensions are 494 x 832 x 832 at scale 10, but 16 x 26 x 26 at scale 5. If we wanted a view volume of, say, k ∈ [127, 145), j ∈ [563, 714), and i ∈ [256, 384) at scale 10, what subvolume would we need to load at scale 5?
To simplify the conceptualization of this problem, it is useful to also shift to a “top-down coordinate system”, which is invariant under a change of scale, as follows: the fundamental voxel is taken to span the interval [0, 1] in each direction.
Now, we know that the original, scale-10 voxmap was not cubical, so how can we have a cubical bounding volume at scale 0? The answer, of course, is that each time we halved a dimension, we rounded up if it was odd. In other words, we effectively padded the scale-10 voxmap out to 1024 x 1024 x 1024 (in general: the smallest power of 2 sufficient to house the largest dimension). Thus, the dimensions of the bounding volume, within the fundamental voxel, should really be considered to be 494/1024 x 832/1024 x 832/1024 (approximately 0.482 x 0.813 x 0.813), rather than 1 x 1 x 1, where the remaining region is just padding.
At the conceptual level, it is useful to represent top-down coordinates in binary, as their representations will always terminate (as the denominator will always be a power of 2). In this case, the bounding volume has dimensions 00.011110111 x 00.1101 x 00.1101. (I denote binary fractions with an extra leading zero before the “binary point”.)
To determine the dimensions of the voxmap we will need at scale n, simply keep n bits of each dimension after the binary point, rounding up. For example, at scale 3 we will need a voxmap of dimensions 00.100 x 00.111 x 00.111.
To determine the array dimensions, simply delete the binary point: 0100 x 0111 x 0111 = 4 x 7 x 7, as obtained above.
Since we know that each array index must be non-negative and less than the array dimension, each top-down voxel coordinate must likewise be non-negative and less than the corresponding dimension of the bounding volume; for our example, z ∈ [0, 00.011110111), y ∈ [0, 00.1101), and x ∈ [0, 00.1101).
For the example above of k ∈ [127, 145), j ∈ [563, 714), and i ∈ [256, 384) at scale 10, we can now write z ∈ [00.0001111111, 00.0010010001), y ∈ [00.1000110011, 00.101100101), and x ∈ [00.01, 00.011). At scale 5, simply retain 5 bits after the binary point, rounding down for the lower bound and rounding up for the upper bound: z ∈ [00.00011, 00.00101), y ∈ [00.10001, 00.10111), and x ∈ [00.01000, 00.01100). The array indices at scale 5 are therefore within the bounds k ∈ [3, 5), j ∈ [17, 23), and i ∈ [8, 12).
Here is a slightly more subtle question: what subvolumes need to be loaded at scales 0 through 4, if we want to load the representation of the object within the subvolume z ∈ [00.00011, 00.00101), y ∈ [00.10001, 00.10111), and x ∈ [00.01000, 00.01100) at scale 5? To answer this, it is necessary to note that Magic Kernel Sharp does not simply replicate each element into the two new elements that it bifurcates into, but it spreads into the neighboring elements; thus, the range of elements that influences a given element at scale n “spreads” as we walk back through the scales < n.
In terms of real-world coding, top-down coordinates can be simply represented as a fixed-point binary fraction, in some unsigned integer type with a suitably large number of bits—say, 32. Then the integer value 0x0000 represents the top-down coordinate 0x.0000, and the integer value 0xffff represents the top-down coordinate 0x.ffff.
© 2010–2023 Dr. John P. Costella